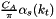uPDFevolv is an evolution code for TMD parton densities using the CCFM evolution equation.
- Authors
- F. Hautmann
Dept. of Physics and Astronomy, University of Sussex,
Rutherford Appleton Laboratory, Dept. of Theoretical Physics,
University of Oxford, UK
-
H. Jung
DESY, Hamburg, FRG,
University of Antwerp, Belgium
-
S. Taheri Monfared
School of Particles and Accelerators, Institute for Research in Fundamental Sciences (IPM), Tehran, Iran
- Version
- 1.0.1
- Date
- 2017
At high energies collisions of hadrons are described by parton densities dependent on the longitudinal momentum fraction 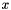 , the transverse momentum
, the transverse momentum 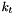 and the evolution scale
and the evolution scale 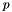 (transverse momentum dependent (TMD) or unintegrated parton density functions (uPDF)). The evolution of the parton density with the scale
(transverse momentum dependent (TMD) or unintegrated parton density functions (uPDF)). The evolution of the parton density with the scale 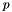 valid at both small and moderate
valid at both small and moderate 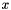 is given by the CCFM evolution equation
is given by the CCFM evolution equation
Theoretical Input
CCFM evolution equation and Transverse Momentum Dependent PDFs
QCD calculations of multiple-scale processes and complex final-states require in general transverse-momentum dependent (TMD), or unintegrated, parton density and parton decay functions[14],[2],[6],[5],[4],[38],[28],[27],[25],[23] . TMD factorization has been proven recently[14]} for inclusive and semi-inclusive deep-inelastic scattering (DIS). For special processes in hadron-hadron scattering, like heavy flavor or heavy boson (including Higgs) production, TMD factorization holds in the high-energy limit (small 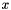 )[11],[12],[26] .
)[11],[12],[26] .
In the framework of high-energy factorization[9],[11] the deep-inelastic scattering cross section can be written as a convolution in both longitudinal and transverse momenta of the TMD parton density function 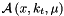 with off-shell partonic matrix elements, as follows
with off-shell partonic matrix elements, as follows
![\[ \sigma_j ( x , Q^2 ) = \int_x^1 d z \int d^2k_t \ \hat{\sigma}_j( x , Q^2 , { z} , k_t ) \ {\cal A}\left( { z} ,k_t, p \right) \hspace*{0.3 cm} (1), \]](form_4.png)
with the DIS cross sections 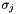 (
( 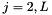 ) related to the structure functions
) related to the structure functions 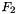 and
and 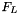 by
by 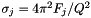 . The hard-scattering kernels
. The hard-scattering kernels 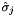 of Eq.(1) are
of Eq.(1) are 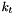 -dependent and the evolution of the transverse momentum dependent gluon density
-dependent and the evolution of the transverse momentum dependent gluon density 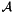 is obtained by combining the resummation of small-
is obtained by combining the resummation of small- 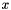 logarithmic contributions[33],[18],[3] with medium-
logarithmic contributions[33],[18],[3] with medium- 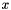 and large-
and large- 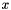 contributions to parton splitting[20],[1],[17] according to the CCFM evolution equation[13],[10][36].
contributions to parton splitting[20],[1],[17] according to the CCFM evolution equation[13],[10][36].
The factorization formula (1) allows one to resum logarithmically enhanced 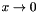 contributions to all orders in perturbation theory, both in the hard scattering coefficients and in the parton evolution, taking fully into account the dependence on the factorization scale
contributions to all orders in perturbation theory, both in the hard scattering coefficients and in the parton evolution, taking fully into account the dependence on the factorization scale 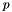 and on the factorization scheme[8],[7].
and on the factorization scheme[8],[7].
The CCFM evolution equation[13],[10],[36] is an exclusive equation for final state partons and includes finite- 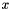 contributions to parton splitting. It incorporates soft gluon coherence for any value of
contributions to parton splitting. It incorporates soft gluon coherence for any value of 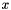 .
.
Gluon distribution
The evolution equation for the TMD gluon density 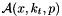 , depending on
, depending on 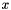 ,
, 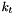 and the evolution variable
and the evolution variable 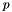 , is
, is
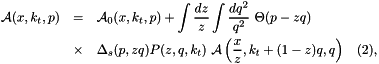
where 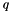 is related to the angle and
is related to the angle and 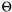 -function specifies the ordering condition of the evolution.
-function specifies the ordering condition of the evolution.
The first term in the right hand side of Eq.(2) is the contribution of the non-resolvable branchings between the starting scale 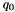 and the evolution scale
and the evolution scale 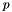 , and is given by
, and is given by
![\[ {\cal A}_0 ( x , k_t , p ) = {\cal A}_0 ( x , k_t , q_0 ) \ \Delta_s (p , q_0) \hspace*{0.3 cm} (3) , \]](form_19.png)
where 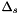 is the Sudakov form factor, and
is the Sudakov form factor, and 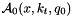 is the starting distribution at scale
is the starting distribution at scale 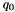 . The integral term in the right hand side of Eq.(2) gives the k_t-dependent branchings in terms of the Sudakov form factor
. The integral term in the right hand side of Eq.(2) gives the k_t-dependent branchings in terms of the Sudakov form factor 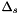 and unintegrated splitting function
and unintegrated splitting function 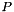 . The Sudakov form factor
. The Sudakov form factor 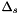 is given by
is given by
![\[ \Delta_s(p,q_0) =\exp{\left( - \int_{q_0^2} ^{p^2} \frac{d q^{2}}{q^{2}} \int_0^{1-q_0/q} dz \ \frac{{\bar \alpha}_s(q^2(1-z)^2)}{1-z} \right)} \hspace*{0.3 cm} (4), \]](form_23.png)
with 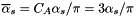 .
.
For application in Monte Carlo event generators, like CASCADE[31],[32], it is of advantage to write the CCFM evolution equation in differential form:
![\[ p^2\frac{d\; }{d p^2} \frac{x {\cal A}(x,k_t,p)}{\Delta_s(p,q_0)}= \int dz \ \frac{d\phi}{2\pi}\, \frac{{P} (z,p/z,k_t)}{\Delta_s(p,q_0)}\, x'{\cal A}(x',k_t',p/z) , \]](form_25.png)
where the splitting variable 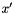 is given by
is given by 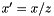 ,
, 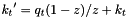 , and
, and 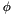 is the azimuthal angle of
is the azimuthal angle of 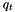 .
.
For the evolution of the parton densities, however, a forward evolution approach, starting from the low scale 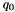 towards the hard scale
towards the hard scale 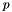 , is used.
, is used.
The splitting function 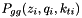 for branching
for branching 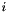 is given by[22] (set by
is given by[22] (set by Ipgg=1, ns=1 in uPDFevolv )
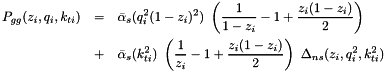
where 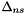 is the non-Sudakov form factor defined by
is the non-Sudakov form factor defined by
![\[ \log\Delta_{ns} = -{\bar \alpha}_s(k^2_{ti}) \int_0^1 dz' \left( \frac{1}{ z'} - 1 + \frac{ z'(1 - z') }{ 2 } \right) \int \frac{d q^2}{q^2} \Theta(k_{ti}-q)\Theta(q-z'q_{ti}). \]](form_35.png)
In addition to the full splitting function, simplified versions are useful in applications and are made available. One uses only the singular parts of the splitting function (set by Ipgg=0, ns=0 in uPDFevolv ):
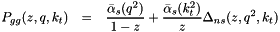
with
![\[ \log\Delta_{ns} = -{\bar \alpha}_s(k^2_{ti}) \int_0^1 \frac{dz'}{ z'} \int \frac{d q^2}{q^2} \Theta(k_{ti}-q)\Theta(q-z'q_{ti}). \]](form_37.png)
Another uses 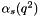 also for the small
also for the small 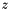 part (set by
part (set by Ipgg=2, ns=2 in uPDFevolv ):
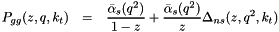
with
![\[ \log\Delta_{ns} = - \int_0^1 \frac{dz'}{ z'} \int \frac{d q^2}{q^2} {\bar \alpha}_s(q^2) \Theta(k_{ti}-q)\Theta(q-z'q_{ti}). \]](form_41.png)
In general a four-momentum 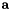 can be written in light-cone variables as
can be written in light-cone variables as 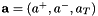 with
with 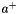 and
and 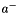 being the light-cone components and
being the light-cone components and 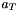 being the transverse component. The CCFM (as well as the BFKL) evolution depends only on one of the light-cone components. Assuming that the other one can be neglected, this leads to the condition that the virtuality of the parton propagator
being the transverse component. The CCFM (as well as the BFKL) evolution depends only on one of the light-cone components. Assuming that the other one can be neglected, this leads to the condition that the virtuality of the parton propagator 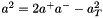 should be dominated by the transverse component, while the contribution from the longitudinal components is required to be small. The condition that
should be dominated by the transverse component, while the contribution from the longitudinal components is required to be small. The condition that 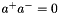 leads to the so-called consistency constraint, which has been implemented in different forms (set by
leads to the so-called consistency constraint, which has been implemented in different forms (set by Ikincut=1,2,3 in uPDFevolv )
Valence quarks
Using the method of[15],[16] valence quarks are included in the branching evolution at the transverse-momentum dependent level according to
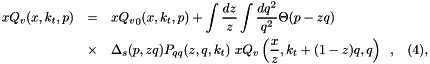
where 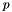 is the evolution scale. The quark splitting function
is the evolution scale. The quark splitting function 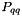 is given by
is given by
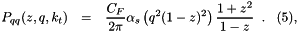
In Eqs.~(4,5) the non-Sudakov form factor is not included, unlike the CCFM kernel given in the appendix~B of[10], because we only associate this factor with 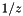 terms. The term
terms. The term 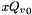 in Eq.~(4) is the contribution of the non-resolvable branchings between starting scale
in Eq.~(4) is the contribution of the non-resolvable branchings between starting scale 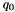 and evolution scale
and evolution scale 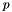 , given by
, given by
![\[ x{ Q_v}_0 (x,k_t,p ) = x{ Q_v}_0 (x,k_t,q_0 ) \Delta_s ( p , q_0) \;\; , \]](form_55.png)
where 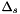 is the Sudakov form factor.
is the Sudakov form factor.
Sea quarks
For a complete description of the final states also the contribution from sea-quarks needs to be included. We include splitting functions 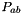 according to
according to
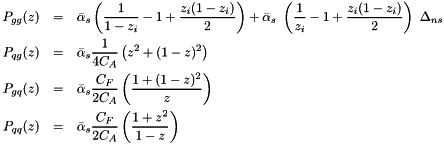
with 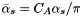 ,
, 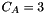 and
and 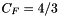 .
.
The 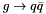 splitting has been calculated in a
splitting has been calculated in a 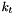 - factorized form in[8],
- factorized form in[8],
![\begin{eqnarray*} P_{qg}( z, {\tilde q}, k_t) & = &{\bar \alpha}_s \frac{1}{4 C_A} \left[ \frac{{\tilde q}^2}{{\tilde q}^2 + z(1-z)\ k_t^2}\right]^2 \left( z^2 + (1-z)^2 + 4 z^2 (1-z)^2 \ \frac{k_t^2}{{\tilde q }^2} \right) \end{eqnarray*}](form_63.png)
with 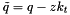 , and
, and 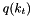 being the transverse momentum of the quark (gluon).
being the transverse momentum of the quark (gluon).
The evolution equation for the TMD sea-quark density 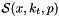 , depending on
, depending on 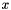 ,
, 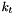 and the evolution variable
and the evolution variable 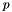 , is
, is
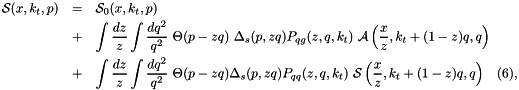
where 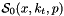 is the non-resolvable branching probability similar to Eqs.(3).
is the non-resolvable branching probability similar to Eqs.(3).
The evolution of the TMD gluon density including the contribution from quarks is given by
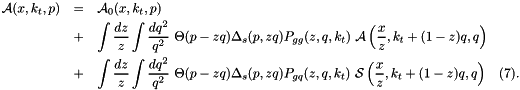
Monte Carlo solution of the CCFM evolution equations
The evolution equations Eqs.(6,7) are integral equations of the Fredholm type
![\[ f(x) = f_0(x) + \lambda \int_a^b K(x,y) f(y) dy \]](form_70.png)
and can be solved by iteration as a Neumann series
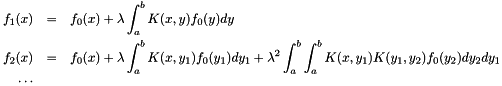
using the kernel 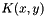 , with the solution
, with the solution
![\[ f(x) = \lim_{n\to \infty} \sum_{i=0}^n f_i(x) . \]](form_73.png)
Applying this to the evolution equations Eqs.(6,7), we identify 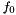 with the first term in eqs.(7), where we use for simplicity here and in the following
with the first term in eqs.(7), where we use for simplicity here and in the following 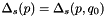 :
:
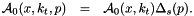
The first iteration involves one branching:
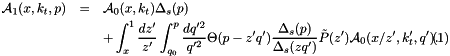
The second iteration involves two branchings,
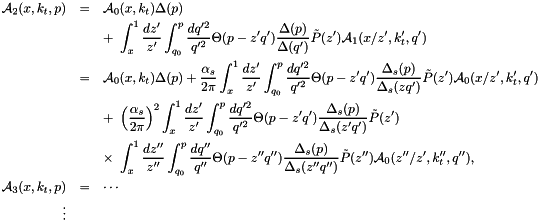
In a Monte Carlo (MC) solution[34],[35] we evolve from 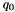 to a value
to a value 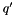 obtained from the Sudakov factor
obtained from the Sudakov factor 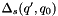 . Note that the Sudakov factor
. Note that the Sudakov factor 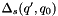 gives the probability for evolving from
gives the probability for evolving from 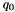 to
to 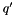 without resolvable branching. The value
without resolvable branching. The value 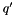 is obtained from solving for
is obtained from solving for 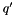 :
:
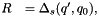
for a random number 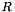 in
in ![$[0,1]$](form_83.png) .
.
If 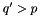 then the scale
then the scale 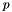 is reached and the evolution is stopped, and we are left with just the first term without any resolvable branching. If
is reached and the evolution is stopped, and we are left with just the first term without any resolvable branching. If 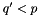 then we generate a branching at
then we generate a branching at 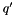 according to the splitting function
according to the splitting function 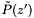 , as described below, and continue the evolution using the Sudakov factor
, as described below, and continue the evolution using the Sudakov factor 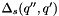 . If
. If 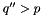 the evolution is stopped and we are left with just one resolvable branching at
the evolution is stopped and we are left with just one resolvable branching at 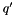 . If
. If 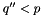 we continue the evolution as described above. This procedure is repeated until we generate
we continue the evolution as described above. This procedure is repeated until we generate 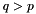 . By this procedure we sum all kinematically allowed contributions in the series
. By this procedure we sum all kinematically allowed contributions in the series 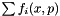 and obtain an MC estimate of the parton distribution function.
and obtain an MC estimate of the parton distribution function.
With the Sudakov factor 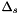 and using
and using
![\begin{eqnarray*} \frac{\partial}{\partial q'^2}\Delta_s(p,zq') = \frac{\partial}{\partial q'^2} \frac{\Delta_s(p)}{\Delta_s(zq')} &=& \frac{\Delta_s(p)}{\Delta_s(zq')} \left[\frac{1}{q'^2}\right] \int^{z_{max}} d z \tilde{P}(z) , \end{eqnarray*}](form_92.png)
we can write the first iteration of the evolution equation as
![\begin{eqnarray*} {\cal A}_1(x,k_t,p) & = & {\cal A}_0 ( x , k_t, p ) \nonumber \\ & + & \int_x^1 \frac{dz'}{z'} \int_{q_0}^p d\Delta_s(p,z'q') \tilde{P}(z') { {\cal A}_0(x/z',k_t',q') } \left[{\int^{z_{max}} d z \tilde{P}(z) } \right]^{-1} . \end{eqnarray*}](form_93.png)
The integrals can be solved by a Monte Carlo method[29] : 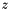 is generated from
is generated from
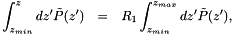
with 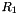 being a random number in
being a random number in ![$[0,1]$](form_83.png) , and
, and 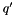 is generated from
is generated from
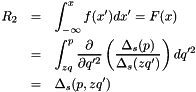
solving for 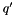 , using
, using 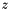 from above and another random number
from above and another random number 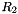 in [0,1].
in [0,1].
This completes the calculation on the first splitting. This procedure is repeated until 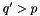 and the evolution is stopped.
and the evolution is stopped.
With 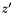 and
and 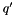 selected according to the above the first iteration of the evolution equation yields
selected according to the above the first iteration of the evolution equation yields
![\begin{eqnarray*} x {\cal A}_1(x,k_t,p) & = & x{\cal A}_0 ( x , k_t ) \Delta_s(p) \nonumber \\ & + & \sum_i \tilde{P}(z'_i) { x'_i{\cal A}_0(x'_i,k'_{t\i},q'_i) } \left[{\int^{z_{max}} d z \tilde{P}(z) } \right]^{-1} , \end{eqnarray*}](form_100.png)
with 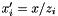 .
.
Normalisation of gluon and quark distributions
The valence quark densities are normalised so that they fulfil for every 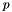 the flavor sum rule.
the flavor sum rule.
The gluon and sea quark densities are normalised so that for every 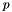
Computational Techniques: CCFM Grid
When using the CCFM evolution in a fit program to determine the starting distribution 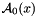 , a full MC solution[34],[35] is no longer suitable, since it is time consuming and suffers from numerical fluctuations. Instead a convolution method introduced in[30][24] is used. The kernel
, a full MC solution[34],[35] is no longer suitable, since it is time consuming and suffers from numerical fluctuations. Instead a convolution method introduced in[30][24] is used. The kernel 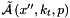 is determined once from the Monte Carlo solution of the CCFM evolution equation, and then folded with the non-perturbative starting distribution
is determined once from the Monte Carlo solution of the CCFM evolution equation, and then folded with the non-perturbative starting distribution 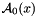 ,
,
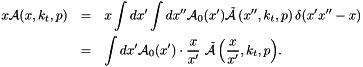
The kernel 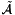 incorporates all of the dynamics of the evolution, including Sudakov form factors and splitting functions. It is determined on a grid of
incorporates all of the dynamics of the evolution, including Sudakov form factors and splitting functions. It is determined on a grid of 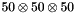 bins in
bins in 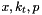 . The binning in the grid is logarithmic, except for the longitudinal variable
. The binning in the grid is logarithmic, except for the longitudinal variable 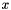 where we use 40 bins in logarithmic spacing below 0.1, and 10 bins in linear spacing above 0.1.
where we use 40 bins in logarithmic spacing below 0.1, and 10 bins in linear spacing above 0.1.
Using this method, the complete coupled evolution of gluon and sea quarks is more complicated, since it is no longer a simple convolution of the kernel with the starting distribution. To simplify the approach, here we allow only for one species of partons at the starting scale, either gluons or sea-quarks. During evolution the other species will be generated. This approach, while convenient for QCD fits, has the feature that sea-quarks, in the case of gluons only at 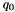 , are generated with perturbative transverse momenta (
, are generated with perturbative transverse momenta ( 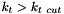 ), without contribution from the soft (non-perturbative) region.
), without contribution from the soft (non-perturbative) region.
Functional Forms for starting distribution
Standard parameterisation
For the starting distribution 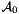 , at the starting scale
, at the starting scale 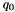 , the following form is used:
, the following form is used:
![\begin{eqnarray*} x{\cal A}_0(x,k_t,q_{0}) = A_1 x^{-A_2} \cdot (1 -x)^{A_3}\left( 1 -A_4 x +A_5 \sqrt{x} +A_6 x^2 \right) \exp[ - k_t^2 / \sigma^2 ] \;\; , \label{a0-5par} \end{eqnarray*}](form_111.png)
with 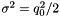 and free parameters
and free parameters  .
.
Valence quarks are treated using the method of[15],[16],[24] with starting distributions at scale 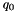 parameterized using standard collinear pdfs (set by
parameterized using standard collinear pdfs (set by Ipdf in uPDFevolv ) as
![\[ x{ Q_v}_0 (x,k_t,q_{0} ) = x{ Q_v}_{\rm{coll. pdf}} (x,q_{0} ) \ \exp[ - k_t^2 / \sigma^2 ] \;\; . \label{gauss} \]](form_115.png)
with 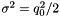 . At every scale
. At every scale 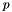 the flavor sum rule is fulfilled for valence quarks.
the flavor sum rule is fulfilled for valence quarks.
Saturation ansatz
A saturation ansatz for the starting distribution 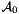 at scale
at scale 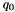 is available, following the parameterisation of the saturation model by Eq.(18) of[19],
is available, following the parameterisation of the saturation model by Eq.(18) of[19],
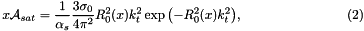
with 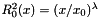 . The free parameters are
. The free parameters are  ,
, 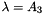 ,
,  and
and 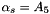 . In order to be able to use this type of parameterisation over the full
. In order to be able to use this type of parameterisation over the full 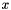 range, an additional factor of
range, an additional factor of 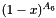 (see[21]) is applied.
(see[21]) is applied.
Plotting TMDs
A simple plot program is included in the package. For a graphical web interface use TMDplotter[37].
Program Installation
uPDFevolv follows the standard AUTOMAKE convention. To install the program, do the following
Get the source
tar xvfz uPDFevolv-XXXX.tar.gz
cd uPDFevolv-XXXX
Generate the Makefiles
Compile the binary
make
make install
The executable is in bin
run it with:
bin/updf_evolve < steer_gluon-JH-2013-set2
plot the result with:
bin/updfread
Acknowledgments
We are very grateful to Bryan Webber for careful reading of the manuscript and clarifying comments.
Subroutines and functions
- routines:
sminit to initialise sminfn to generate starting distributions in 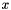 and
and 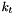
smbran to simulate perturbative branchings splittgg to generate 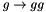 splitting via
splitting via 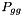
splittgq to generate 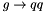 splitting via
splitting via 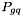
splittqg to generate 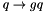 splitting via
splitting via 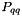
splittqq to generate 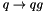 splitting via
splitting via 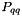
szvalnew to calculate 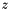 values for
values for 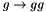 splitting
splitting smqtem to generate $t$ from the corresponding Sudakov factor updfgrid to build, fill and normalise the updf grid. asbmy(kt) to calculate 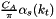
- Utility routines:
evolve tmd Main routine to perform CCFM evolution updfread example program to read and plot the results gadap 1-dimensional Gauss integration routine gadap2 2-dimensional Gauss integration routine divdif linear interpolation routine (CERNLIB) ranlux Random number generator RANLUX (CERNLIB)
 1.8.3.1
1.8.3.1
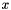 , the transverse momentum
, the transverse momentum 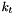 and the evolution scale
and the evolution scale 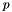 (transverse momentum dependent (TMD) or unintegrated parton density functions (
(transverse momentum dependent (TMD) or unintegrated parton density functions (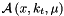 with off-shell partonic matrix elements, as follows
with off-shell partonic matrix elements, as follows ![\[ \sigma_j ( x , Q^2 ) = \int_x^1 d z \int d^2k_t \ \hat{\sigma}_j( x , Q^2 , { z} , k_t ) \ {\cal A}\left( { z} ,k_t, p \right) \hspace*{0.3 cm} (1), \]](form_4.png)
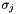 (
( 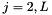 ) related to the structure functions
) related to the structure functions 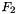 and
and 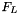 by
by 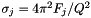 . The hard-scattering kernels
. The hard-scattering kernels 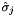 of Eq.(1) are
of Eq.(1) are 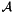 is obtained by combining the resummation of small-
is obtained by combining the resummation of small- 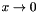 contributions to all orders in perturbation theory, both in the hard scattering coefficients and in the parton evolution, taking fully into account the dependence on the factorization scale
contributions to all orders in perturbation theory, both in the hard scattering coefficients and in the parton evolution, taking fully into account the dependence on the factorization scale 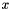 contributions to parton splitting. It incorporates soft gluon coherence for any value of
contributions to parton splitting. It incorporates soft gluon coherence for any value of 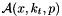 , depending on
, depending on 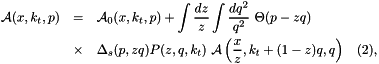
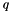 is related to the angle and
is related to the angle and 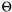 -function specifies the ordering condition of the evolution.
-function specifies the ordering condition of the evolution.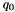 and the evolution scale
and the evolution scale ![\[ {\cal A}_0 ( x , k_t , p ) = {\cal A}_0 ( x , k_t , q_0 ) \ \Delta_s (p , q_0) \hspace*{0.3 cm} (3) , \]](form_19.png)
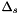 is the Sudakov form factor, and
is the Sudakov form factor, and 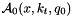 is the starting distribution at scale
is the starting distribution at scale 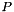 . The Sudakov form factor
. The Sudakov form factor ![\[ \Delta_s(p,q_0) =\exp{\left( - \int_{q_0^2} ^{p^2} \frac{d q^{2}}{q^{2}} \int_0^{1-q_0/q} dz \ \frac{{\bar \alpha}_s(q^2(1-z)^2)}{1-z} \right)} \hspace*{0.3 cm} (4), \]](form_23.png)
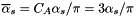 .
.![\[ p^2\frac{d\; }{d p^2} \frac{x {\cal A}(x,k_t,p)}{\Delta_s(p,q_0)}= \int dz \ \frac{d\phi}{2\pi}\, \frac{{P} (z,p/z,k_t)}{\Delta_s(p,q_0)}\, x'{\cal A}(x',k_t',p/z) , \]](form_25.png)
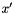 is given by
is given by 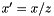 ,
, 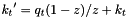 , and
, and 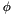 is the azimuthal angle of
is the azimuthal angle of 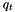 .
.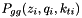 for branching
for branching 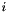 is given by
is given by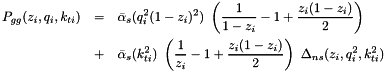
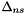 is the non-Sudakov form factor defined by
is the non-Sudakov form factor defined by ![\[ \log\Delta_{ns} = -{\bar \alpha}_s(k^2_{ti}) \int_0^1 dz' \left( \frac{1}{ z'} - 1 + \frac{ z'(1 - z') }{ 2 } \right) \int \frac{d q^2}{q^2} \Theta(k_{ti}-q)\Theta(q-z'q_{ti}). \]](form_35.png)
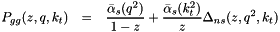
![\[ \log\Delta_{ns} = -{\bar \alpha}_s(k^2_{ti}) \int_0^1 \frac{dz'}{ z'} \int \frac{d q^2}{q^2} \Theta(k_{ti}-q)\Theta(q-z'q_{ti}). \]](form_37.png)
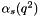 also for the small
also for the small 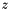 part (set by
part (set by 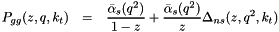
![\[ \log\Delta_{ns} = - \int_0^1 \frac{dz'}{ z'} \int \frac{d q^2}{q^2} {\bar \alpha}_s(q^2) \Theta(k_{ti}-q)\Theta(q-z'q_{ti}). \]](form_41.png)
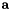 can be written in light-cone variables as
can be written in light-cone variables as 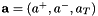 with
with 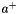 and
and 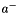 being the light-cone components and
being the light-cone components and 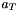 being the transverse component. The CCFM (as well as the BFKL) evolution depends only on one of the light-cone components. Assuming that the other one can be neglected, this leads to the condition that the virtuality of the parton propagator
being the transverse component. The CCFM (as well as the BFKL) evolution depends only on one of the light-cone components. Assuming that the other one can be neglected, this leads to the condition that the virtuality of the parton propagator 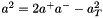 should be dominated by the transverse component, while the contribution from the longitudinal components is required to be small. The condition that
should be dominated by the transverse component, while the contribution from the longitudinal components is required to be small. The condition that 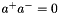 leads to the so-called consistency constraint, which has been implemented in different forms (set by
leads to the so-called consistency constraint, which has been implemented in different forms (set by 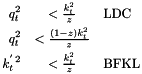
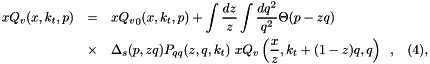
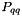 is given by
is given by 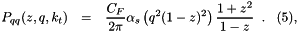
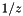 terms. The term
terms. The term 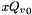 in Eq.~(4) is the contribution of the non-resolvable branchings between starting scale
in Eq.~(4) is the contribution of the non-resolvable branchings between starting scale ![\[ x{ Q_v}_0 (x,k_t,p ) = x{ Q_v}_0 (x,k_t,q_0 ) \Delta_s ( p , q_0) \;\; , \]](form_55.png)
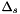 is the Sudakov form factor.
is the Sudakov form factor. 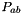 according to
according to 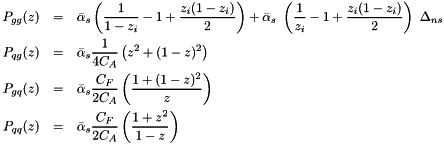
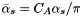 ,
, 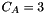 and
and 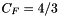 .
.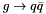 splitting has been calculated in a
splitting has been calculated in a ![\begin{eqnarray*} P_{qg}( z, {\tilde q}, k_t) & = &{\bar \alpha}_s \frac{1}{4 C_A} \left[ \frac{{\tilde q}^2}{{\tilde q}^2 + z(1-z)\ k_t^2}\right]^2 \left( z^2 + (1-z)^2 + 4 z^2 (1-z)^2 \ \frac{k_t^2}{{\tilde q }^2} \right) \end{eqnarray*}](form_63.png)
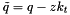 , and
, and 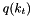 being the transverse momentum of the quark (gluon).
being the transverse momentum of the quark (gluon).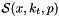 , depending on
, depending on 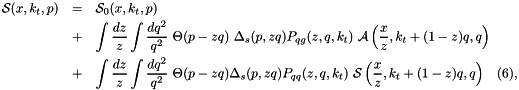
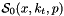 is the non-resolvable branching probability similar to Eqs.(3).
is the non-resolvable branching probability similar to Eqs.(3).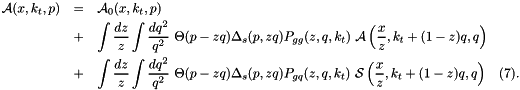
![\[ f(x) = f_0(x) + \lambda \int_a^b K(x,y) f(y) dy \]](form_70.png)
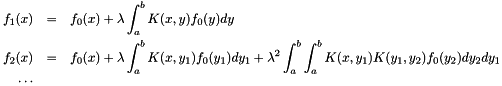
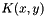 , with the solution
, with the solution ![\[ f(x) = \lim_{n\to \infty} \sum_{i=0}^n f_i(x) . \]](form_73.png)
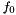 with the first term in eqs.(7), where we use for simplicity here and in the following
with the first term in eqs.(7), where we use for simplicity here and in the following 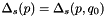 :
: 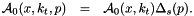
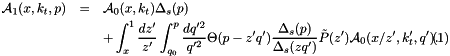
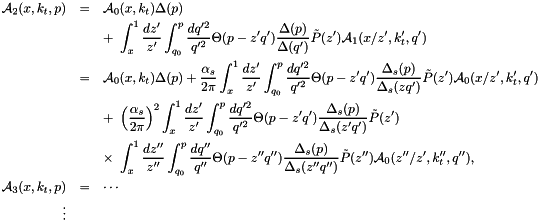
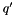 obtained from the Sudakov factor
obtained from the Sudakov factor 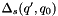 . Note that the Sudakov factor
. Note that the Sudakov factor 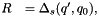
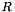 in
in ![$[0,1]$](form_83.png) .
.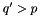 then the scale
then the scale 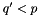 then we generate a branching at
then we generate a branching at 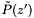 , as described below, and continue the evolution using the Sudakov factor
, as described below, and continue the evolution using the Sudakov factor 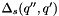 . If
. If 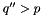 the evolution is stopped and we are left with just one resolvable branching at
the evolution is stopped and we are left with just one resolvable branching at 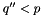 we continue the evolution as described above. This procedure is repeated until we generate
we continue the evolution as described above. This procedure is repeated until we generate 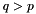 . By this procedure we sum all kinematically allowed contributions in the series
. By this procedure we sum all kinematically allowed contributions in the series 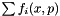 and obtain an MC estimate of the parton distribution function.
and obtain an MC estimate of the parton distribution function.![\begin{eqnarray*} \frac{\partial}{\partial q'^2}\Delta_s(p,zq') = \frac{\partial}{\partial q'^2} \frac{\Delta_s(p)}{\Delta_s(zq')} &=& \frac{\Delta_s(p)}{\Delta_s(zq')} \left[\frac{1}{q'^2}\right] \int^{z_{max}} d z \tilde{P}(z) , \end{eqnarray*}](form_92.png)
![\begin{eqnarray*} {\cal A}_1(x,k_t,p) & = & {\cal A}_0 ( x , k_t, p ) \nonumber \\ & + & \int_x^1 \frac{dz'}{z'} \int_{q_0}^p d\Delta_s(p,z'q') \tilde{P}(z') { {\cal A}_0(x/z',k_t',q') } \left[{\int^{z_{max}} d z \tilde{P}(z) } \right]^{-1} . \end{eqnarray*}](form_93.png)
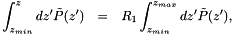
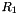 being a random number in
being a random number in 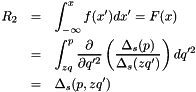
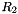 in [0,1].
in [0,1].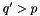 and the evolution is stopped.
and the evolution is stopped.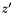 and
and ![\begin{eqnarray*} x {\cal A}_1(x,k_t,p) & = & x{\cal A}_0 ( x , k_t ) \Delta_s(p) \nonumber \\ & + & \sum_i \tilde{P}(z'_i) { x'_i{\cal A}_0(x'_i,k'_{t\i},q'_i) } \left[{\int^{z_{max}} d z \tilde{P}(z) } \right]^{-1} , \end{eqnarray*}](form_100.png)
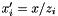 .
.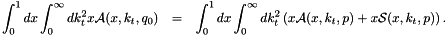
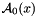 , a full MC solution
, a full MC solution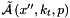 is determined once from the Monte Carlo solution of the CCFM evolution equation, and then folded with the non-perturbative starting distribution
is determined once from the Monte Carlo solution of the CCFM evolution equation, and then folded with the non-perturbative starting distribution 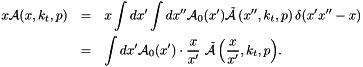
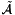 incorporates all of the dynamics of the evolution, including Sudakov form factors and splitting functions. It is determined on a grid of
incorporates all of the dynamics of the evolution, including Sudakov form factors and splitting functions. It is determined on a grid of 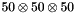 bins in
bins in 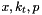 . The binning in the grid is logarithmic, except for the longitudinal variable
. The binning in the grid is logarithmic, except for the longitudinal variable 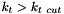 ), without contribution from the soft (non-perturbative) region.
), without contribution from the soft (non-perturbative) region.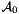 , at the starting scale
, at the starting scale ![\begin{eqnarray*} x{\cal A}_0(x,k_t,q_{0}) = A_1 x^{-A_2} \cdot (1 -x)^{A_3}\left( 1 -A_4 x +A_5 \sqrt{x} +A_6 x^2 \right) \exp[ - k_t^2 / \sigma^2 ] \;\; , \label{a0-5par} \end{eqnarray*}](form_111.png)
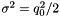 and free parameters
and free parameters  .
.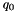 parameterized using standard collinear pdfs (set by
parameterized using standard collinear pdfs (set by ![\[ x{ Q_v}_0 (x,k_t,q_{0} ) = x{ Q_v}_{\rm{coll. pdf}} (x,q_{0} ) \ \exp[ - k_t^2 / \sigma^2 ] \;\; . \label{gauss} \]](form_115.png)
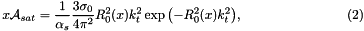
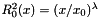 . The free parameters are
. The free parameters are  ,
, 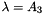 ,
,  and
and 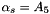 . In order to be able to use this type of parameterisation over the full
. In order to be able to use this type of parameterisation over the full 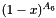 (see
(see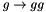 splitting via
splitting via 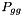
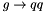 splitting via
splitting via 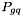
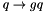 splitting via
splitting via 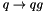 splitting via
splitting via 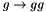 splitting
splitting